Sample Size and Decision Rules
A number of decisions have to be made when testing for inter-coder agreement. For instance, how much data material needs to be used, how many instances need to be coded with any given code for the calculation to be possible, and how to evaluate the obtained coefficient.
Sample size
The data you use for the ICA analysis needs to be representative of the total amount of data you have collected, thus of those data whose reliability is in question. Furthermore, the number of codings per code needs to be sufficiently high. As a rule of thumb, the codings per code should at least yield five agreements by chance.
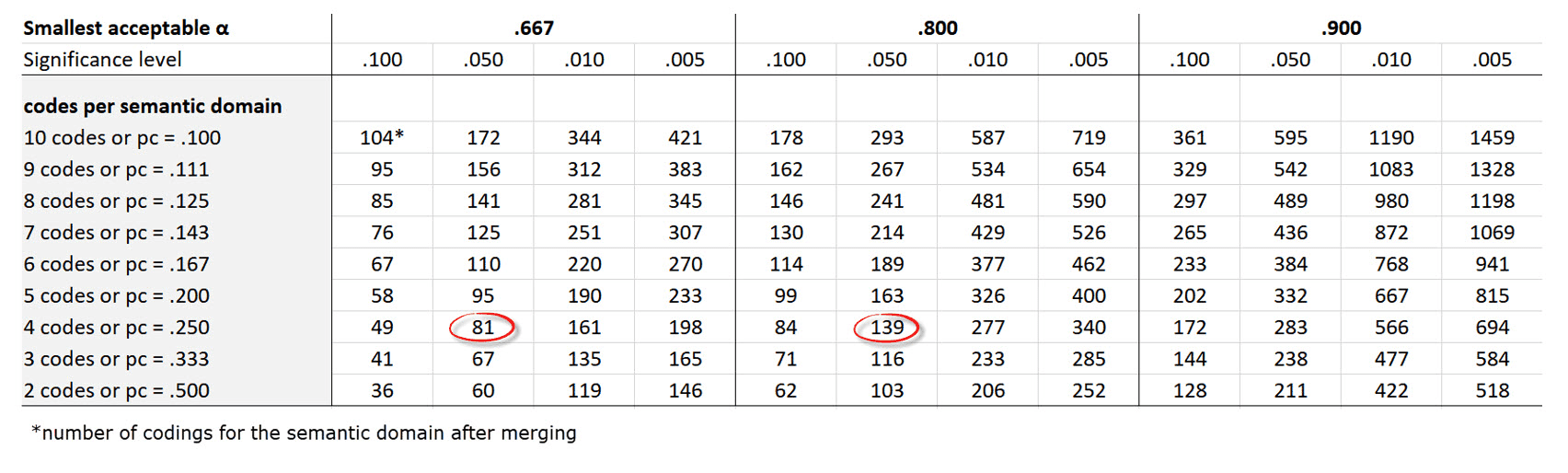
Krippendorff (2019) uses Bloch and Kraemer's formula 3.7 (1989:276) to obtain the required sample size. The table below lists the sample size you need when working with two coders:
-
the three smallest acceptable reliabilities α min: 0.667 / 0.800 / 0.900
-
for four levels of statistical significance: 0.100 / 0.050 / 0.010 / 0.005
-
for semantic domains up to 10 codes (=probability pc):
Example: If you have a semantic domain with 4 codes and each of the codes are equally distributed (pc = 1/4 = 0,25), and if the minimum alpha should be 0.800 at a 0.05 level of statistical significance, you need a minimum of 139 codings for this semantic domain. For a lower alpha of 0.667, you need a minimum of 81 codings at the same level of statistical significance.
 It applies to 2 coders, and for semantic domains up to 10 sub-codes. If you have more than two coders, more than 10 sub-codes in a domain, or an unequal distribution within a domain, you need to adjust the equation and calculate the needed sample size yourself.
It applies to 2 coders, and for semantic domains up to 10 sub-codes. If you have more than two coders, more than 10 sub-codes in a domain, or an unequal distribution within a domain, you need to adjust the equation and calculate the needed sample size yourself.
-
More than two coders: You need to and multiply Z square by the number of coders.
-
More than 10 sub-codes per domain: You need to adjust the value for pc. The value for pc = 1/number of sub-codes.
-
Unequal distribution of codings within a domain: By 4 codes in a semantic domain, the estimated proportion pc of all values c in the population is 0.250 (¼); by 5 codes, it is 0,200 (1/5); by 6 codes 0,167 (1/6) and so on. If the distribution of your codes in a semantic domain is unequal, you need to make a new estimate for the sample size by using a pc in the formula that is correspondingly less than 1/4, 1/5, 1/6 and so on.
You can see the corresponding z value from a standard normal distribution table. For a p-value of 0,05, z = 1,65.
Acceptable Level of Reliability
The last question to consider is when to accept or reject coded data based on the ICA coefficient. Krippendorff (2019) recommends:
- Strive to reach α = 1,000, even if this is just an ideal.
- Do not accept data with reliability values below α = 0.667.
- In most cases, you can consider a semantic domain to be reliable if α ≥ 0.800.
- Select at least 0.05 as the statistical level of significance to minimize the risk of a Type 1 error, which is to accept data as reliable if this is not the case.
Which cut-off point you choose always depends on the validity requirements that are placed on the research results. If the result of your analysis affects or even jeopardizes someone's life, you should use more stringent criteria. A cut-off point of α = 0.800 means that 80% of the data is coded to a degree better than chance. If you are satisfied with α = 0.500, this means 50% of your data is coded to a degree better than chance. The sounds a bit like tossing a coin and playing heads or tails.